algorithmdata-structurestreeheaptreap

priority generation in treap data structure

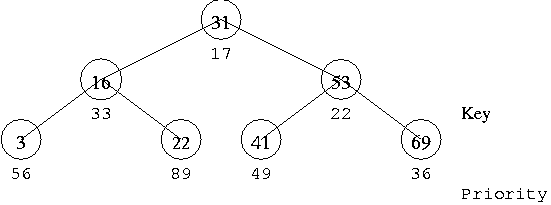
treap example

I'm studying the treap data structure. When inserting node, treap radomly generate node's priority. But what if 69 node's generated priority is 13 in the picture above?

Parent's priority must higher than child's priority. Do treap's binary tree attribute collide with heap attribute?

I want to know. Thanks.

Solution

  • Assuming you have treap from your picture without 69 node and want to add (69, 13) node:
    1. Split existing treap to 2 treaps L and R by key 69 (here all old treap will be L)
    2. Create treap M with single node (69, 13)
    3. Merge M with L, then result with R
    For this case node (69, 13) becomes a new root, and old treap will be it's left child.