Bootstrapping a vector of results, by group in R

Question: How can I use a boostrap to get confidence intervals for a collection of statistics calculated on the eigenvalues of covariance matrices, separately for each group (factor level) in a data frame?

Problem: I can't quite work out the data structure I need to contain these results suitable for the boot function, or a way to "map" the bootstrap over groups and obtain confidence intervals in a form suitable for plotting.

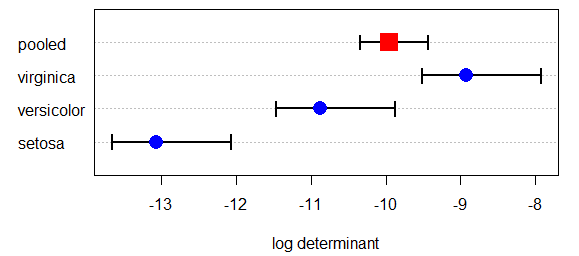
Context: In the heplots package, boxM calculates Box's M test of equality of covariance matrices. There is a plot method that produces a useful plot of the log determinants that go into this test. The confidence intervals in this plot are based on an asymptotic theory approximation.

> library(heplots)
> iris.boxm <- boxM(iris[, 1:4], iris[, "Species"])
> iris.boxm

        Box's M-test for Homogeneity of Covariance Matrices

data:  iris[, 1:4]
Chi-Sq (approx.) = 140.94, df = 20, p-value < 2.2e-16

> plot(iris.boxm, gplabel="Species")

The plot method can also display other functions of the eigenvalues, but no theoretical confidence intervals are available in this case.

op <- par(mfrow=c(2,2), mar=c(5,4,1,1))
plot(iris.boxm, gplabel="Species", which="product")
plot(iris.boxm, gplabel="Species", which="sum")
plot(iris.boxm, gplabel="Species", which="precision")
plot(iris.boxm, gplabel="Species", which="max")
par(op)

Thus, I would like to be able to calculate these CIs using a boostrap, and display them in the corresponding plots.

What I've tried:

Below are functions that boostrap these statistics, but for the total sample, not taking group (Species) into account.

cov_stat_fun <- function(data, indices, 
            stats=c("logdet", "prod", "sum", "precision", "max")
            ) {
    dat <- data[indices,]
    cov <- cov(dat, use="complete.obs")
    eigs <- eigen(cov)$values

    res <- c(
        "logdet" = log(det(cov)),
        "prod" = prod(eigs),
        "sum" = sum(eigs),
        "precision" = 1/ sum(1/eigs),
        "max" = max(eigs)
        )
}

boot_cov_stat <- function(data, R=500,  ...) {
    boot(data, cov_stat_fun, R=R,  ...)
}

This works, but I need the results by group (and also for the total sample)

> iris.boot <- boot_cov_stat(iris[,1:4])
>
> iris.ci <- boot.ci(iris.boot)
> iris.ci
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot)

Intervals : 
Level      Normal              Basic             Studentized     
95%   (-6.622, -5.702 )   (-6.593, -5.653 )   (-6.542, -5.438 )  

Level     Percentile            BCa          
95%   (-6.865, -5.926 )   (-6.613, -5.678 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
>

I also have written a function that calculates the separate covariance matrices for each group, but I can't see how to use this in my bootstrap functions. Can someone help?

# calculate covariance matrices by group and pooled
covs <- function(Y, group) {
   Y <- as.matrix(Y)
   gname <- deparse(substitute(group))
   if (!is.factor(group)) group <- as.factor(as.character(group))

   valid <- complete.cases(Y, group)
   if (nrow(Y) > sum(valid)) 
      warning(paste(nrow(Y) - sum(valid)), " cases with missing data have been removed.")
   Y <- Y[valid,]
   group <- group[valid]
   nlev <- nlevels(group)
   lev <- levels(group)
   mats <- aux <- list()
   for(i in 1:nlev) {
      mats[[i]] <- cov(Y[group == lev[i], ])
   }
   names(mats) <- lev
   pooled <- cov(Y)
   c(mats, "pooled"=pooled)
}

Edit: In a seemingly related question, Bootstrap by groups, it is suggested that an answer is provided by using the strata argument to boot(), but there is no example of what this gives. [Ah: the strata argument just assures that strata are represented in the bootstrap sample in relation to their frequencies in the data.]

Trying this for my problem, I am not further enlightened, because what I want to get is separate confidence intervals for each Species.

> iris.boot.strat <- boot_cov_stat(iris[,1:4], strata=iris$Species)
> 
> boot.ci(iris.boot.strat, conf=0.95, type=c("basic", "bca"))
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot.strat, conf = 0.95, type = c("basic", 
    "bca"))

Intervals : 
Level      Basic                BCa          
95%   (-6.587, -5.743 )   (-6.559, -5.841 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
> 

If I understand your question, you can run your bootstrap function by group as follows:

library(boot)
library(tidyverse)

# Pooled
iris.boot <- boot_cov_stat(iris[,1:4])
iris.ci <- boot.ci(iris.boot)

# By Species
boot.list = setNames(unique(iris$Species), unique(iris$Species)) %>% 
  map(function(group) {
    iris.boot = boot_cov_stat(iris[iris$Species==group, 1:4])
    boot.ci(iris.boot)
  })

# Combine pooled and by-Species results
boot.list = c(boot.list, list(Pooled=iris.ci))

boot.list

$setosa
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot)

Intervals : 
Level      Normal              Basic             Studentized     
95%   (-13.69, -11.86 )   (-13.69, -11.79 )   (-13.52, -10.65 )  

Level     Percentile            BCa          
95%   (-14.34, -12.44 )   (-13.65, -11.99 )  
Calculations and Intervals on Original Scale
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable

$versicolor
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot)

Intervals : 
Level      Normal              Basic             Studentized     
95%   (-11.37,  -9.81 )   (-11.36,  -9.78 )   (-11.25,  -8.97 )  

Level     Percentile            BCa          
95%   (-11.97, -10.39 )   (-11.35, -10.09 )  
Calculations and Intervals on Original Scale
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable

$virginica
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot)

Intervals : 
Level      Normal              Basic             Studentized     
95%   (-9.467, -7.784 )   (-9.447, -7.804 )   (-9.328, -6.959 )  

Level     Percentile            BCa          
95%   (-10.050,  -8.407 )   ( -9.456,  -8.075 )  
Calculations and Intervals on Original Scale
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable

$Pooled
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 500 bootstrap replicates

CALL : 
boot.ci(boot.out = iris.boot)

Intervals : 
Level      Normal              Basic             Studentized     
95%   (-6.620, -5.714 )   (-6.613, -5.715 )   (-6.556, -5.545 )  

Level     Percentile            BCa          
95%   (-6.803, -5.906 )   (-6.624, -5.779 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable