pythonmathematical-optimizationmystic

How to find the parameter to optimize (maximize) the expected value of a function with random variable globally (using python mystic)

I'm new in asking at StackOverflow so sorry if using it in a wrong manner.

I have a maximize problem in a paper just like this:

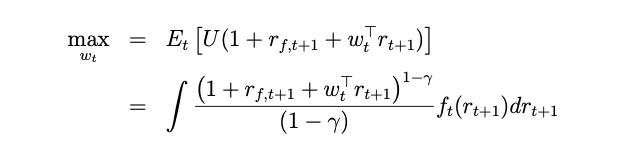
CRRA.png

and some constraints:

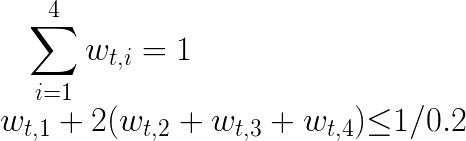
CodeCogsEqn.png

where r_f,t+1 and γ are given constant, r_t+1 is a multidimensional random variable vector(4 dimension here), f_t(r_t+1) is the multidimensional distribution function of the r_t+1. The problem is to find a weight vector w_t to maximize the expected value.

The paper said how it solves the problem, "The integrals are solved by simulating 100,000 variates for the 4 factors(the r_t+1 vector) from the multivariate conditional return distribution f_t(rt+1)". I know how to generate random numbers and get the mean from a distribution, but don't exactly know about how to use it in an optimization problem.

I have tried using some random numbers and return the mean value as the objective function, like the example below:

import numpy as np
rands = np.random.multivariate_normal(mean=[0, 0, 0, 0],
                                      cov=[[1, 0, 0, 0], [0, 1, 0, 0],
                                           [0, 0, 1, 0], [0, 0, 0, 1]],
                                      size=1000)


def expect_value(weight, rf, gamma, fac_ndarr):
    weight = np.asarray(weight)
    utility_array = (1 + rf + fac_ndarr.dot(weight))**(1 - gamma) / (1 - gamma)

    expected_value = utility_array.mean()
    return -expected_value

And the next, I use the module mystic to solve the global minimum.

from mystic.solvers import diffev2
from mystic.symbolic import (generate_conditions, generate_penalty,
                             generate_constraint, generate_solvers, simplify)

equation = """
x0 + x1 + x2 + x3 == 1
x0 + 2*(x1 + x2 + x3) - (1. / 0.2) <= 0
"""

pf = generate_penalty(generate_conditions(equation), k=1e20)
cf = generate_constraint(generate_solvers(simplify(equation)))
bounds = [(0, 1)] * 4

# Here the given constant `rf` and `gamma` are 0.15 and 7, 
# and they were passed to the parameter `args` with `rands`, 
# the `args` will be passed to the `cost`funtion.
result = diffev2(cost=expect_value,
                 args=(0.15, 7, rands),
                 x0=bounds,
                 bounds=bounds,
                 constraint=cf,
                 penalty=pf,
                 full_output=True,
                 npop=40)

My real problem generated 50000 random numbers, and it seems can't find the exact global minimum solution, since every time the code finds a different solution and the value of objective function differs. And even after reading the documentation and changing the parameter "npop" to 1000 and the "scale"(multiplier for mutations on the trial solution) to 0.1, it also didn't work as expected.

Is the way I used to solve the optimization problem wrong? What is the exact way to use simulation data in maximizing an expected value? Or there's something wrong in using the mystic module? Or, is there another efficient way to solve the maximization problem like above?

Thanks very much for your help！

Solution

  • mystic is built for this exact type of problem, as it can optimize in product measure space. See: https://github.com/uqfoundation/mystic/blob/master/examples5/TEST_OUQ_surrogate_diam.py