LSTM 'recurrent_dropout' with 'relu' yields NaNs

Any non-zero recurrent_dropout yields NaN losses and weights; latter are either 0 or NaN. Happens for stacked, shallow, stateful, return_sequences = any, with & w/o Bidirectional(), activation='relu', loss='binary_crossentropy'. NaNs occur within a few batches.

Any fixes? Help's appreciated.

---

TROUBLESHOOTING ATTEMPTED:

• recurrent_dropout=0.2,0.1,0.01,1e-6
• kernel_constraint=maxnorm(0.5,axis=0)
• recurrent_constraint=maxnorm(0.5,axis=0)
• clipnorm=50 (empirically determined), Nadam optimizer
• activation='tanh' - no NaNs, weights stable, tested for up to 10 batches
• lr=2e-6,2e-5 - no NaNs, weights stable, tested for up to 10 batches
• lr=5e-5 - no NaNs, weights stable, for 3 batches - NaNs on batch 4
• batch_shape=(32,48,16) - large loss for 2 batches, NaNs on batch 3

NOTE: batch_shape=(32,672,16), 17 calls to train_on_batch per batch

---

ENVIRONMENT:

• Keras 2.2.4 (TensorFlow backend), Python 3.7, Spyder 3.3.7 via Anaconda
• GTX 1070 6GB, i7-7700HQ, 12GB RAM, Win-10.0.17134 x64
• CuDNN 10+, latest Nvidia drives

---

ADDITIONAL INFO:

Model divergence is spontaneous, occurring at different train updates even with fixed seeds - Numpy, Random, and TensorFlow random seeds. Furthermore, when first diverging, LSTM layer weights are all normal - only going to NaN later.

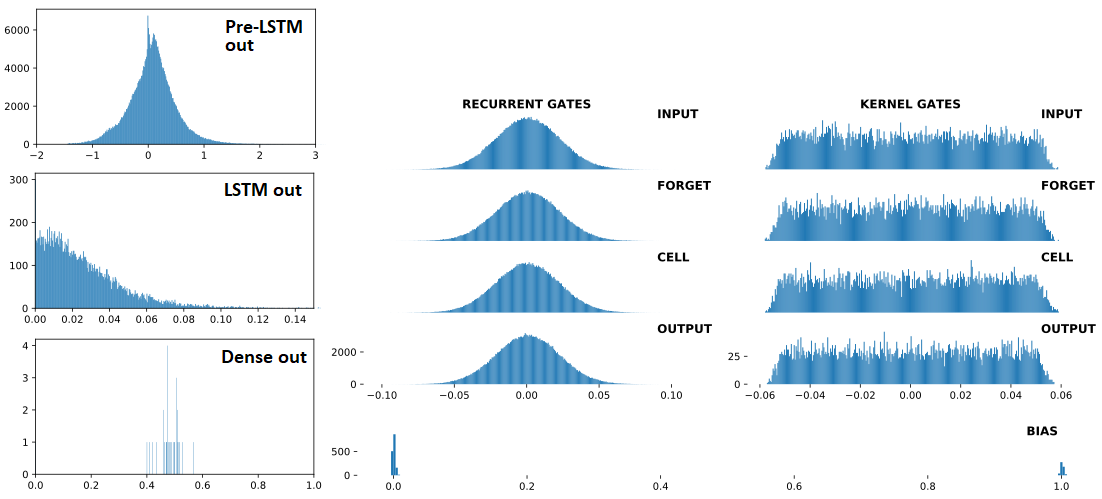
Below are, in order: (1) inputs to LSTM; (2) LSTM outputs; (3) Dense(1,'sigmoid') outputs -- the three are consecutive, with Dropout(0.5) between each. Preceding (1) are Conv1D layers. Right: LSTM weights. "BEFORE" = 1 train update before; "AFTER = 1 train update after

BEFORE divergence:

AT divergence:

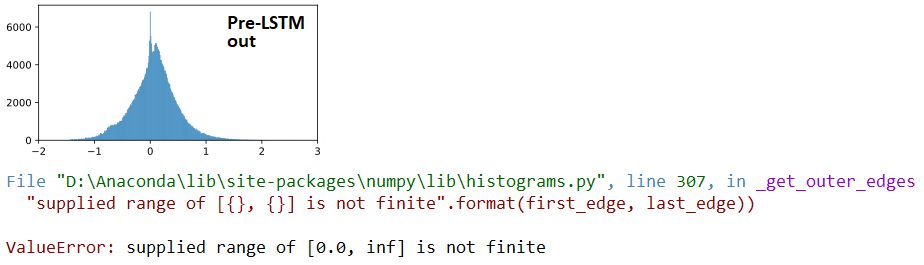
## LSTM outputs, flattened, stats
(mean,std)        = (inf,nan)
(min,max)         = (0.00e+00,inf)
(abs_min,abs_max) = (0.00e+00,inf)

AFTER divergence:

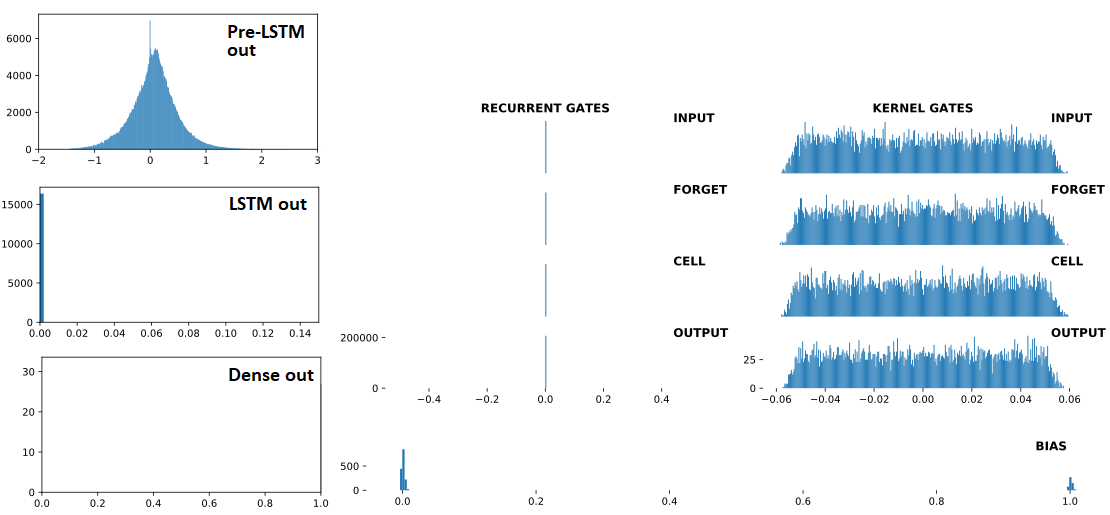
## Recurrent Gates Weights:
array([[nan, nan, nan, ..., nan, nan, nan],
       [ 0.,  0., -0., ..., -0.,  0.,  0.],
       [ 0., -0., -0., ..., -0.,  0.,  0.],
       ...,
       [nan, nan, nan, ..., nan, nan, nan],
       [ 0.,  0., -0., ..., -0.,  0., -0.],
       [ 0.,  0., -0., ..., -0.,  0.,  0.]], dtype=float32)
## Dense Sigmoid Outputs:
array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
        1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]], dtype=float32)

---

MINIMAL REPRODUCIBLE EXAMPLE:

from keras.layers import Input,Dense,LSTM,Dropout
from keras.models import Model
from keras.optimizers  import Nadam 
from keras.constraints import MaxNorm as maxnorm
import numpy as np

ipt = Input(batch_shape=(32,672,16))
x = LSTM(512, activation='relu', return_sequences=False,
              recurrent_dropout=0.3,
              kernel_constraint   =maxnorm(0.5, axis=0),
              recurrent_constraint=maxnorm(0.5, axis=0))(ipt)
out = Dense(1, activation='sigmoid')(x)

model = Model(ipt,out)
optimizer = Nadam(lr=4e-4, clipnorm=1)
model.compile(optimizer=optimizer,loss='binary_crossentropy')

for train_update,_ in enumerate(range(100)):
    x = np.random.randn(32,672,16)
    y = np.array([1]*5 + [0]*27)
    np.random.shuffle(y)
    loss = model.train_on_batch(x,y)
    print(train_update+1,loss,np.sum(y))

Observations: the following speed up divergence:

• Higher units (LSTM)
• Higher # of layers (LSTM)
• Higher lr << no divergence when <=1e-4, tested up to 400 trains
• Less '1' labels << no divergence with y below, even with lr=1e-3; tested up to 400 trains

y = np.random.randint(0,2,32) # makes more '1' labels

---

UPDATE: not fixed in TF2; reproducible also using from tensorflow.keras imports.

Studying LSTM formulae deeper and digging into the source code, everything's come crystal clear.

Verdict: recurrent_dropout has nothing to do with it; a thing's being looped where none expect it.

---

Actual culprit: the activation argument, now 'relu', is applied on the recurrent transformations - contrary to virtually every tutorial showing it as the harmless 'tanh'.

I.e., activation is not only for the hidden-to-output transform - source code; it operates directly on computing both recurrent states, cell and hidden:

c = f * c_tm1 + i * self.activation(x_c + K.dot(h_tm1_c, self.recurrent_kernel_c))
h = o * self.activation(c)

---

Solution(s):

• Apply BatchNormalization to LSTM's inputs, especially if previous layer's outputs are unbounded (ReLU, ELU, etc)
  • If previous layer's activations are tightly bounded (e.g. tanh, sigmoid), apply BN before activations (use activation=None, then BN, then Activation layer)
• Use activation='selu'; more stable, but can still diverge
• Use lower lr
• Apply gradient clipping
• Use fewer timesteps

---

More answers, to some remaining questions:

• Why was recurrent_dropout suspected? Unmeticulous testing setup; only now did I focus on forcing divergence without it. It did however, sometimes accelerate divergence - which may be explained by by it zeroing the non-relu contributions that'd otherwise offset multiplicative reinforcement.
• Why do nonzero mean inputs accelerate divergence? Additive symmetry; nonzero-mean distributions are asymmetric, with one sign dominating - facilitating large pre-activations, hence large ReLUs.
• Why can training be stable for hundreds of iterations with a low lr? Extreme activations induce large gradients via large error; with a low lr, this means weights adjust to prevent such activations - whereas a high lr jumps too far too quickly.
• Why do stacked LSTMs diverge faster? In addition to feeding ReLUs to itself, LSTM feeds the next LSTM, which then feeds itself the ReLU'd ReLU's --> fireworks.

---

UPDATE 1/22/2020: recurrent_dropout may in fact be a contributing factor, as it utilizes inverted dropout, upscaling hidden transformations during training, easing divergent behavior over many timesteps. Git Issue on this here