QR-Factorization in least square sense to solve A * w = b

I'm trying to implement the QR24-Algorithm to calibrate flange/tool and robot/world from this paper by Floris Ernst (2012).

I need to solve an equation M_i*X - Y*N_i = 0 where M_i and N_i are known and i from 1 to the number of measurements and X and Y are unknown Matrices.

In the paper they combined this equation into a system of linear equations A*w = b, where A consists of 12*number of measurements rows and 24 columns, so I have a system of linear equations with 24 parameters, where I need at least 2 measurements to solve this system.

To solve this equation, I need to use the QR-Factorization in least square sense because with more measurements, this system has more equations than parameters.

I'm using the OLSMultipleLinearRegression from the Apache Commons Math library to solve the equation system:

OLSMultipleLinearRegression regression = new OLSMultipleLinearRegression();
regression.setNoIntercept(true);
regression.newSampleData(B.toArray(), A.getData());
RealVector w = new ArrayRealVector(regression.estimateRegressionParameters());

The RealVector w now should contain the entries for the unknown matrices X and Y (without the last row, which is always [0 0 0 1], because those matrices are homogeneous transformation matrices).

I generated some test measurement data by hand on paper using Denavit-Hartenberg, because I have currently no access to the robot and tracking system I want to use, because of corona.

However, my result X and Y Matrices (Vector w) I get are always so absurd and very very far away from the results I'm expecting. For example, when I use exact transformation matrices without any translational or rotational error (besides computational error from my computer), I get for the rotational part of my matrices values more than 10^14 (which obviously can't be true) and for translational part more than 10^17 instead of expected 100 or so.

When I add some measurement errors to my matrices (for example +-0.01° in rotation and +-0.01 for translational part), I don't get those super high values, but values for the rotational part that nevertheless can't be true.

Have you any idea, why those values are so very wrong, or any advice how to use QR-factorization in least square sense with this library?

Here's also my code to create each entry/submatrix Ai of A using the M_i and N_i measurement:

private RealMatrix createAi(RealMatrix m,RealMatrix n, boolean invert) {
    RealMatrix M = new Array2DRowRealMatrix();
    if(invert) {
         M = new QRDecomposition(m).getSolver().getInverse();
    }else {
        M = m.copy();
    }
    // getRot is a method i wrote to get the rotational part of a matrix
    RealMatrix RM = getRot(M);
    
    RealMatrix N = n.copy();
    // 12 equations per Measurement and 24 parameters to solve for
    RealMatrix Ai = new Array2DRowRealMatrix(12,24);
    RealMatrix Zero = new Array2DRowRealMatrix(3,3);
    RealMatrix Identity12 = MatrixUtils.createRealIdentityMatrix(12);
    
    // first column
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(0, 0)).getData(), 0, 0);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(0, 1)).getData(), 3, 0);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(0, 2)).getData(), 6, 0);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(0, 3)).getData(), 9, 0);
                                                       
    // secondcolumn
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(1, 0)).getData(), 0, 3);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(1, 1)).getData(), 3, 3);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(1, 2)).getData(), 6, 3);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(1, 3)).getData(), 9, 3);

    // third column
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(2, 0)).getData(), 0, 6);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(2, 1)).getData(), 3, 6);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(2, 2)).getData(), 6, 6);
    Ai.setSubMatrix(RM.scalarMultiply(N.getEntry(2, 3)).getData(), 9, 6);
    
    // fourth column
    Ai.setSubMatrix(Zero.getData(), 0, 9);
    Ai.setSubMatrix(Zero.getData(), 3, 9);
    Ai.setSubMatrix(Zero.getData(), 6, 9);
    Ai.setSubMatrix(RM.getData(), 9, 9);
    
    // fifth column
    Ai.setSubMatrix(Identity12.scalarMultiply(-1d).getData(), 0, 12);
    return Ai;
}

And here's my code to create each entry/subvector bi of b using the M_i measurement:

private RealVector createBEntry(RealMatrix m, boolean invert) {
    RealMatrix bi = new Array2DRowRealMatrix(1,12);
    RealMatrix negative_M = new Array2DRowRealMatrix();
    // getTrans is a method i wrote to get the translational part of a matrix
    if(invert) {
        negative_M = getTrans(new QRDecomposition(m).getSolver().getInverse()).scalarMultiply(-1d); 
    }else {
        negative_M = getTrans(m).scalarMultiply(-1d);
    }       
    bi.setSubMatrix(negative_M.getData(), 0, 9);
    
    return bi.getRowVector(0);
}

I was able to find a solution to my problem and I want to share it with you. The problem was not a programming error, but the paper provided an incorrect matrix (the Ai matrix) which is needed to solve the linear system of equations. I tried to extract a system of linear equations from M*X - Y*N = 0 by myself using the characteristics of homogeneous transformation matrices and rotation matrices. I came up with following solution:

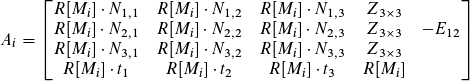
where

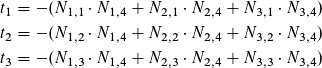
The vector bi provided in the paper is fine.

Since Prof. Ernst teaches at my university and I'm taking a course with him, I will try to make him aware of the mistake.