GPS distance: Pythagora's on an Equirectangular approximation vs Haversine fomula errors at different scales?

I'm trying to decide whether it makes cpu processing time sense to use the more complex Haversine formula instead of the faster Pythagorean's formula but while there seems to be a pretty unanimous answer on the lines of: "you can use Pythagora's formula for acceptable results on small distances but haversine is better", I can not find even a vague definition on what "small distances" mean.

This page, linked in the top answer to the very popular question Calculate distance between two latitude-longitude points? claims:

If performance is an issue and accuracy less important, for small distances Pythagoras’ theorem can be used on an equi­rectangular projec­tion:*

Accuracy is somewhat complex: along meridians there are no errors, otherwise they depend on distance, bearing, and latitude, but are small enough for many purposes*

the asterisc even says "Anyone care to quantify them?"

But this answer claims that the error is about 0.1% at 1000km (but it doesn't cite any reference, just personal observations) and that for 4km (even assuming the % doesn't shrink due to way smaller distance) it would mean under 4m of error which for public acces GPS is around the open-space best gps accuracy.

Now, I don't know what the average Joe thinks of when they say "small distances" but for me, 4km is definitely not a small distance (- I'm thinking more of tens of meters), so I would be grateful if someone can link or calculate a table of errors just like the one in this answer of Measuring accuracy of latitude and longitude? but I assume the errors would be higher near the poles so maybe choose 3 representative lattitudes (5*, 45* and 85*?) and calculate the error with respect to the decimal degree place.

Of course, I would also be happy with an answer that gives an exact meaning to "small distances".

Yes ... at 10 meters and up to 1km meters you're going to be very accurate using plain old Pythagoras Theorem. It's really ridiculous nobody talks about this, especially considering how much computational power you save.

Proof: Take the top of the earth, since it will be a worst case, the top 90 miles longitude, so that it's a circle with the longitudinal lines intersecting in the middle.

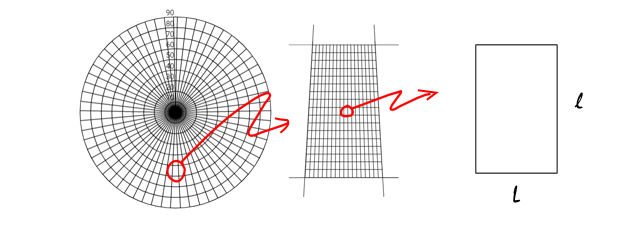
Note above that as you zoom in to an area as small as 1km, just 50 miles from the poles, what originally looked like a trapezoid with curved top and bottom borders, essentially looks like a nearly perfect rectangle. In other words we can assume rectilinearity at 1km, and especially at a mere 10M.

Now, its true of course that the longitude degrees are much shorter near the poles than at the equator. For example any slack-jawed yokel can see that the rectangles made by the latitude and longitude lines grow taller, the aspect ratio increasing, as you get closer to the poles. In fact the relationship of the longitude distance is simply what it would be at the equator multiplied by the cosine of the latitude of anywhere along the path. ie. in the image above where "L" (longitude distance) and "l" (latitude distance) are both the same degrees it is:

LATcm = Latitude at *any* point along the path (because it's tiny compared to the earth)

L = l * cos(LATcm)

Thus, we can for 1km or less (even near the poles) calculate the distance very accurately using Pythagoras Theorem like so:

 Where: latitude1, longitude1 = polar coordinates of the start point

 and:   latitude2, longitude2 = polar coordinates of the end point

distance = sqrt((latitude2-latitude1)^2 + ((longitude2-longitude1)*cos(latitude1))^2) * 111,139*60

Where 111,139*60 (above) is the number of meters within one degree at the equator,
because we have to convert the result from equator degrees to meters.

A neat thing about this is that GPS systems usually take measurements at about 10m or less, which means you can get very accurate over very large distances by summing up the results from this equation. As accurate as Haversine formula. The super-tiny errors don't magnify as you sum up the total because they are a percentage that remains the same as they are added up.

Reality is however that the Haversine formula (which is very accurate) isn't difficult, but relatively speaking Haversine will consume your processor at least 3 times more, and up to 31x more computational intensive according to this guy: https://blog.mapbox.com/fast-geodesic-approximations-with-cheap-ruler-106f229ad016.

For me this formula did come useful to me when I was using a system (Google sheets) that couldn't give me the significant digits that are necessary to do the haversine formula.