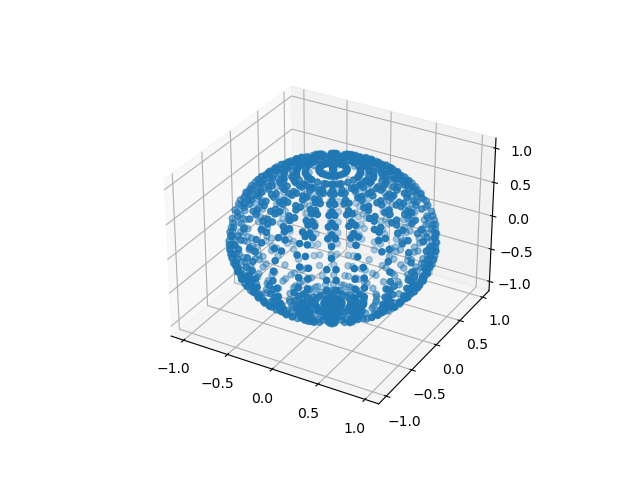
How to generate points on spherical surface making equal parts?

I would like to generate a sphere containing n euqal parts. For example, I want to divide my spherical surface into 36 X 36 parts. Therefore, it should contain 1296 equal parts in total. I do not have clue how to generate points in spherical (3D) space.

I want my plot looking like this but in place of line, I want only point (where two lines intersect).

I know only formulas mentioned below,

X = R * np.sin(PHI) * np.cos(THETA)
Y = R * np.sin(PHI) * np.sin(THETA)
Z = R * np.cos(PHI)

How would I generate points make equal parts in sphere?

• to make phi and theta vary along [0,180] and [0,360]: use numpy.linspace.

• to get all possible combinations of cos(phi) * cos(theta): use the outer product numpy.outer.

• to split along equal angles, use z = sin(phi); to split into rectangles of equal area, split equally along the z-axis.

import numpy as np

def split_sphere(R = 1, horizontal_split = 36, vertical_split = 36, method="equal_angles"):
    theta = np.linspace(0,360,horizontal_split+1)
    if method == "equal_angles":
        phi = np.linspace(0, 180, vertical_split+1)
        c = np.cos(phi)
        s = np.sin(phi)
    elif method == "equal_area":
        c = np.linspace(-1, 1, vertical_split+1)
        s = 1 - c**2
    else:
        raise(ValueError('method must be "equal_angles" or "equal_area"'))
    x = R * np.outer(s, np.cos(theta))
    y = R * np.outer(s, np.sin(theta))
    z = R * np.outer(c, np.ones(horizontal_split+1))
    return x, y, z

def main():
    import matplotlib.pyplot as plt
    x,y,z = split_sphere()
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    ax.scatter(x,y,z)
    plt.show()

if __name__=='__main__':
    main()