pythondictionarytriangulationdelaunay

Harvest data and attributes from Shewchuk's Triangle

Lets say I have an area with regions and I execute a constrained Delaunay with Rufat's implementation of Shewchuk's Triangle (python)

import numpy as np
import triangle as tr
import matplotlib.pyplot as plt

# data
vertices = [[0, 0], [5, 0], [5, 5], [0, 5],
            [1, 1], [2, 1], [2, 2], [1, 2],
           [3, 3], [4, 3], [4, 4], [3, 4],
           [2, 3], [1, 3],
           [4, 1], [4, 2]]
segments = [[0, 1], [1, 2], [2, 3], [3, 0],
           [4, 5], [5, 6], [6, 7], [7, 4],
           [8, 9], [9, 10], [10, 11], [11, 8],
           [6, 12], [12, 13], [7, 13],
           [5, 14], [14, 15], [6, 15]]
regions = [[1.5, 1.5, 1, 0],
          [3.5, 3.5, 3, 0],
          [1.5, 2.5, 2, 0],
          [3, 1.5, 4, 0],]

A = dict(vertices=vertices, segments=segments, regions=regions)
B = tr.triangulate(A, 'pAn')
    
tr.compare(plt, A, B)
plt.show()

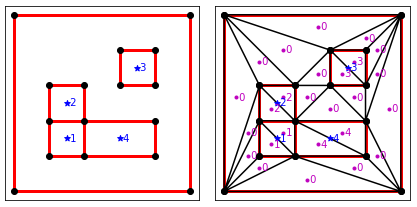
image

with the dict B looking like:

{'vertices': array([[0., 0.],
        [5., 0.],
        [5., 5.],
        [0., 5.],
        ...
        [1., 3.],
        [4., 1.],
        [4., 2.]]),
 'vertex_markers': array([[1],
        [1],
        [1],
        [1],
       ...
        [0],
        [0],
        [0]], dtype=int32),
 'triangles': array([[ 0,  4,  7],
        [ 4,  0,  5],
        [ 7,  5,  6],
        [ 5,  7,  4],
        ...
        [ 2, 10,  9],
        [ 9, 15,  2],
        [11,  2,  3],
        [ 8, 11, 12]], dtype=int32),
 'triangle_attributes': array([[0.],
        [0.],
        [1.],
        [1.],
        ...
        [0.],
        [0.],
        [0.]]),
 'neighbors': array([[ 3,  5,  1],
        [ 4,  3,  0],
        [12, 10,  3],
        ...
        [15, 22, 18],
        [-1, 11, 21],
        [11,  9, 20]], dtype=int32),
 'segments': array([[ 1,  0],
        [ 2,  1],
        [ 3,  2],
        ...
        [ 5, 14],
        [14, 15],
        [ 6, 15]], dtype=int32),
 'segment_markers': array([[1],
        [1],
        [1],
        [1],
        ...
        [0],
        [0]], dtype=int32),
 'regions': array([[1.5, 1.5, 1. , 0. ],
        [3.5, 3.5, 3. , 0. ],
        [1.5, 2.5, 2. , 0. ],
        [3. , 1.5, 4. , 0. ]])}

i) How do I iterate each region 1-4 (not 0);
ii) harvest each segment that bounds the region;
iii) extract the coordinates of the 2 vertices of each segment; along with
iv) the attribute of that region plus the attribute of the region on the other side of the segment?

Thufar I have:

# get the segments that bound each region
for i, region in enumerate(regions):
    region_triangles = np.where(Tr['triangle_attributes'] == i+1)[0]
    region_segments = []
    for tri in region_triangles:
        tri_vertices = Tr['triangles'][tri]
        for j in range(3):
            seg = sorted([tri_vertices[j], tri_vertices[(j+1)%3]])
            if seg not in region_segments:
                if seg in segments:
                    region_segments.append(seg)
    print("Region", i+1, "is bounded by segments:", region_segments)

    # get the coordinates of the vertices that form each segment
    segment_vertices = []
    for seg in region_segments:
        v1 = Tr['vertices'][seg[0]]
        v2 = Tr['vertices'][seg[1]]
        segment_vertices.append((v1, v2))
    print("Vertices of the segments that bound region", i+1, ":", segment_vertices)

    # get the neighboring regions of each segment
    segment_neighbors = []
    for seg in region_segments:
        neighbors = []
        for j, reg in enumerate(regions):
            if j != i:
                reg_triangles = np.where(Tr['triangle_attributes'] == j+1)[0]
                for tri in reg_triangles:
                    tri_vertices = Tr['triangles'][tri]
                    if seg[0] in tri_vertices and seg[1] in tri_vertices:
                        neighbors.append(j+1)
                        break
        segment_neighbors.append(neighbors)
    print("Neighboring regions of the segments that bound region", i+1, ":", segment_neighbors)
    print('')

which yields:

Region 1 is bounded by segments: [[5, 6], [6, 7], [4, 5]]
Vertices of the segments that bound region 1 : [(array([2., 1.]), array([2., 2.])), (array([2., 2.]), array([1., 2.])), (array([1., 1.]), array([2., 1.]))]
Neighboring regions of the segments that bound region 1 : [[4], [2], []]

Region 2 is bounded by segments: [[6, 12], [12, 13], [7, 13], [6, 7]]
Vertices of the segments that bound region 2 : [(array([2., 2.]), array([2., 3.])), (array([2., 3.]), array([1., 3.])), (array([1., 2.]), array([1., 3.])), (array([2., 2.]), array([1., 2.]))]
Neighboring regions of the segments that bound region 2 : [[], [], [], [1]]

Region 3 is bounded by segments: [[9, 10], [10, 11], [8, 9]]
Vertices of the segments that bound region 3 : [(array([4., 3.]), array([4., 4.])), (array([4., 4.]), array([3., 4.])), (array([3., 3.]), array([4., 3.]))]
Neighboring regions of the segments that bound region 3 : [[], [], []]

Region 4 is bounded by segments: [[5, 14], [5, 6], [6, 15], [14, 15]]
Vertices of the segments that bound region 4 : [(array([2., 1.]), array([4., 1.])), (array([2., 1.]), array([2., 2.])), (array([2., 2.]), array([4., 2.])), (array([4., 1.]), array([4., 2.]))]
Neighboring regions of the segments that bound region 4 : [[], [1], [], []]

Region 1 and 3 is incorrect

Solution

  • you need to check if the segments go in the other direction

    if seg in segments or [seg[1], seg[0]] in segments:

    so the code would be:

    # get the segments that bound each region
for i, region in enumerate(regions):
    region_triangles = np.where(Tr['triangle_attributes'] == i+1)[0]
    region_segments = []
    for tri in region_triangles:
        tri_vertices = Tr['triangles'][tri]
        for j in range(3):
            seg = sorted([tri_vertices[j], tri_vertices[(j+1)%3]])
            if seg not in region_segments:
                if seg in segments or [seg[1], seg[0]] in segments:
                    region_segments.append(seg)
    print("Region", i+1, "is bounded by segments:", region_segments)

    # get the coordinates of the vertices that form each segment
    segment_vertices = []
    segment_neighbors = []
    for seg in region_segments:
        v1 = Tr['vertices'][seg[0]]
        v2 = Tr['vertices'][seg[1]]
        #-- check direction of normals point outward from bld.
        if np.cross(v2 - v1, region[:2] - v1) < 0:
            seg = seg[::-1]
            segment_vertices.append((v2, v1))
        else:
            segment_vertices.append((v1, v2))
        # get the neighboring regions of each segment
        neighbors = []
        for j, reg in enumerate(regions):
            if j != i:
                reg_triangles = np.where(Tr['triangle_attributes'] == j+1)[0]
                for tri in reg_triangles:
                    tri_vertices = Tr['triangles'][tri]
                    if seg[0] in tri_vertices and seg[1] in tri_vertices:
                        neighbors.append(j+1)
                        break
        segment_neighbors.append(neighbors)
    print("Vertices of the segments that bound region", i+1, ":", segment_vertices)
    print("Neighboring regions of the segments that bound region", i+1, ":", segment_neighbors)
    print('')

    Region 1 is bounded by segments: [[5, 6], [6, 7], [4, 7], [4, 5]]
Vertices of the segments that bound region 1 : [(array([2., 1.]), array([2., 2.])), (array([2., 2.]), array([1., 2.])), (array([1., 2.]), array([1., 1.])), (array([1., 1.]), array([2., 1.]))]
Neighboring regions of the segments that bound region 1 : [[4], [2], [], []]

Region 2 is bounded by segments: [[6, 12], [12, 13], [7, 13], [6, 7]]
Vertices of the segments that bound region 2 : [(array([2., 3.]), array([2., 2.])), (array([1., 3.]), array([2., 3.])), (array([1., 3.]), array([1., 2.])), (array([1., 2.]), array([2., 2.]))]
Neighboring regions of the segments that bound region 2 : [[], [], [], [1]]

Region 3 is bounded by segments: [[9, 10], [10, 11], [8, 11], [8, 9]]
Vertices of the segments that bound region 3 : [(array([4., 3.]), array([4., 4.])), (array([4., 4.]), array([3., 4.])), (array([3., 3.]), array([3., 4.])), (array([4., 3.]), array([3., 3.]))]
Neighboring regions of the segments that bound region 3 : [[], [], [], []]

Region 4 is bounded by segments: [[5, 14], [5, 6], [6, 15], [14, 15]]
Vertices of the segments that bound region 4 : [(array([2., 1.]), array([4., 1.])), (array([2., 2.]), array([2., 1.])), (array([4., 2.]), array([2., 2.])), (array([4., 1.]), array([4., 2.]))]
Neighboring regions of the segments that bound region 4 : [[], [1], [], []]