matlabmatlab-figure

Patching a color gradient with respect to given angular data

I am trying to patch a color gradient of given angular data

Here is the data:

n = [263.6909 287.9987 262.1933 199.6890 128.5683 71.1718 34.6535 15.2568 6.2683 2.4868 0.9872 0.4063 0.1793 0.0876 0.0487 0.0315 0.0241 0.0221 0.0243 0.0319 0.0495 0.0895 0.1838 0.4174 1.0159 2.5605 6.4504 15.6740 35.5053  72.6566 130.6707 201.9328];

theta=0:(2*pi/32):(2*pi*(32-1)/32);
theta(theta>pi) = theta(theta>pi)-2*pi;

I use a patch command

figure
hold on
patch(cos(theta), sin(theta), n, 'EdgeColor', 'none');
quiver(0,0,-4.6492,-0.9099,0.5,'k','linewidth',3);
axis equal

** edit start 3/12/2024 **

The gradient is suppose to be perpendicular to the line between the peak of the concentration and the opposite point along the rim (i.e, from $\theta(n_{max})$ and $\theta(n_{max}+\pi)).

There are two options I'm trying to apply:

1.Assuming that there is an exponential decaying gradient where the gradient patch decays from n_max to zero in the vertical direction.

  1. fitting a Gaussian to the data and use that with a corresponding theta which is segmented equally with respect to the location of the peak (i.e, one of the array point of theta is exactly where the peak is).

** edit end 3/12/2024 **

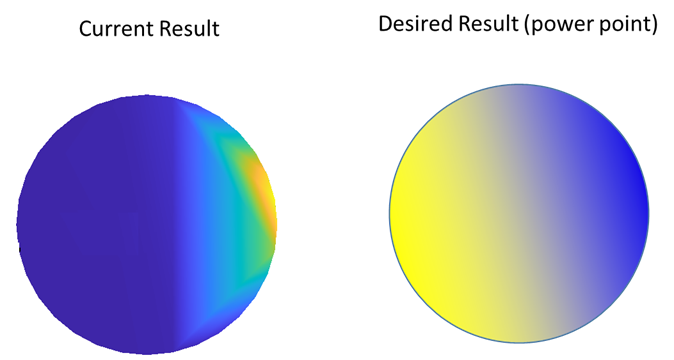
Here in the plot below is what I obtain, and what I wish to obtain

enter image description here

I highlight that the data is part of a dynamical simulation where the array n changes every iteration, and therefore the gradient slope, and direction, must be according to the given n

Solution

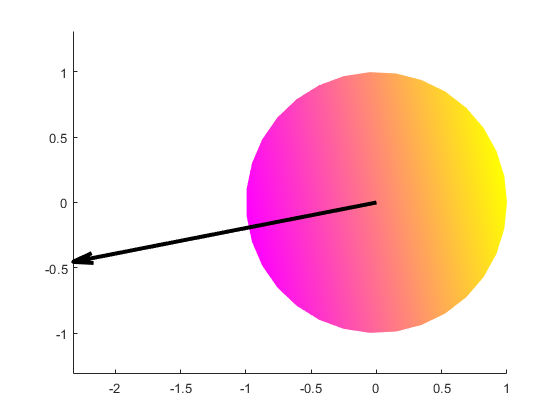
  • Your vector n is not smooth, and doesn't represent a parallel gradient to any vector direction. You can see this by just using plot(n), it aligns with the representation you get. This code shows how you can plot a gradient perpendicular to a given vector:

    You can use atan2 to work out the direction of your vector aUV, and set the colour equal to cos(theta + aUV + pi/2), since you want to start drawing the colours offset by aUV from where you're drawing the circular patch and the additional pi/2 makes the gradient perpendicular.

    % Some setup values
N = 32;        % Number of samples in array
U = -4.6492;   % X displacement of vector
V = -0.9099;   % Y displacement of vector
% Calculate circle drawing vectors
aUV = atan2(U,V);              % Angle of UV vector
theta = linspace(0,2*pi,N);    % Angle array for drawing patch
clr = cos(theta + aUV + pi/2); % Offset cyclic colour starting from aUV+pi/2
% Plot
figure(1); clf; hold on;
patch(cos(theta), sin(theta), clr, 'EdgeColor', 'none');
quiver(0,0,U,V,0.5,'k','linewidth',3);
axis equal; colormap spring

    Output:

    output plot

    Edit with respect to question update... If you do not have the angle or direction vector as an input we can determine it from the input n by

    See the code comments for details

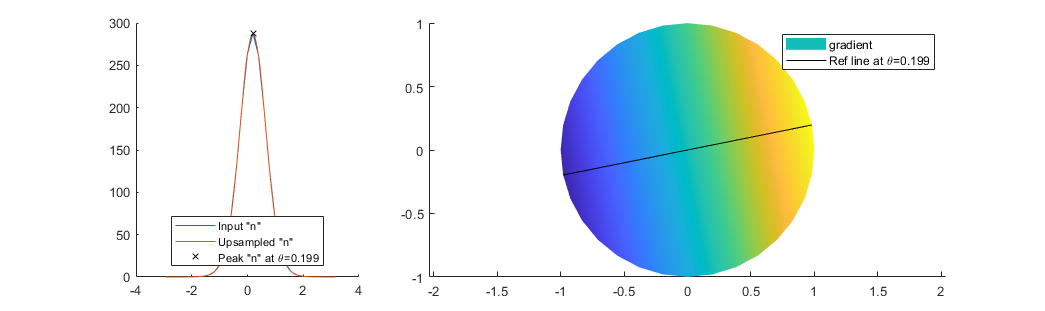
    % Sort theta so that we can interpolate with it as the axis
[theta,idx] = sort(theta);
n = n(idx); % Match the order of points in 'n' with sorted theta
% Upsample 'n' using piecewise cubic interpolation
theta_i = linspace(theta(1),theta(end),1000);
n_i = interp1( theta, n, theta_i, 'pchip' );
% Find the index for the max value of 'n'
[n_max,idx] = max(n_i);
aUV = theta_i(idx);

% Offset cyclic colour starting from aUV
clr = cos(theta - aUV); 

% Plotting... side by side of input curve with gradient for comparison
label = sprintf('\\theta=%.3f',aUV); % helper for legend labelling
figure(1); clf;                      

subplot(1,3,1); hold on;
plot(theta,n,'displayname','Input "n"');
plot(theta_i,n_i,'displayname','Upsampled "n"');
plot(aUV,n_max,'kx','displayname',['Peak "n" at ' label]);
legend('show','location','south');

subplot(1,3,2:3); hold on;
patch(cos(theta), sin(theta), clr, 'EdgeColor', 'none','displayname','gradient');
line( [-1,1]*cos(aUV), [-1,1]*sin(aUV), 'color', 'k', 'displayname', ['Ref line at ' label]);
axis equal; colormap parula; legend show

    Result:

    updated plot