PCA after k-means clustering of multidimensional data

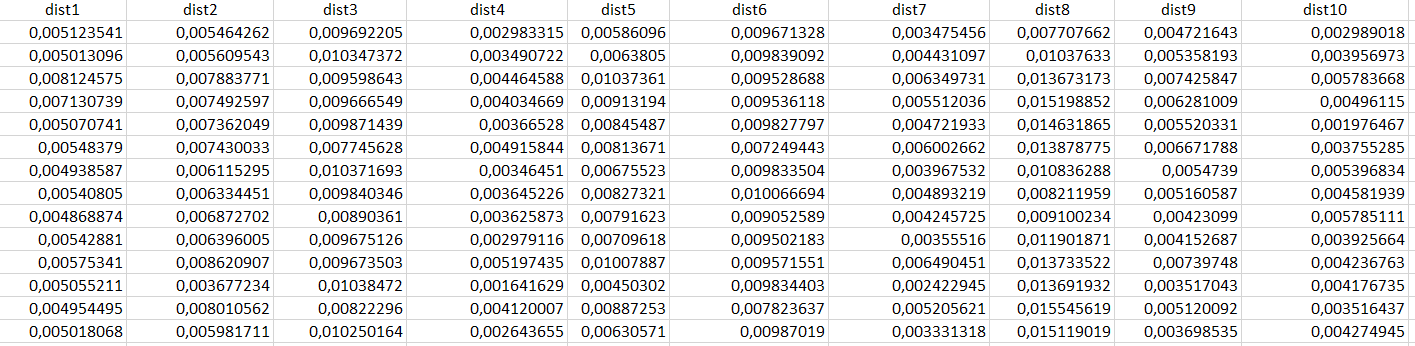
I have the following dataset with 10 variables:

I want to identify clusters with this multidimensional dataset, so I tried k-means clustering algorith with the following code:

clustering_kmeans = KMeans(n_clusters=2, precompute_distances="auto", n_jobs=-1)
data['clusters'] = clustering_kmeans.fit_predict(data)

In order to plot the result I used PCA for dimensionality reduction:

reduced_data = PCA(n_components=2).fit_transform(data)
results = pd.DataFrame(reduced_data,columns=['pca1','pca2'])
sns.scatterplot(x="pca1", y="pca2", hue=kmeans['clusters'], data=results)
plt.title('K-means Clustering with 2 dimensions')
plt.show()

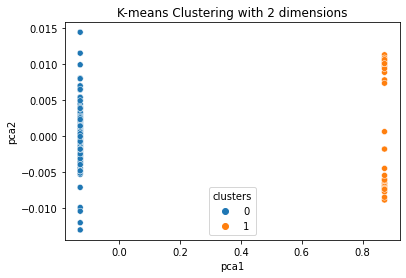
And in the end I get the following result:

So I have the following questions:

1. However, this PCA plot looks really weird splitting the whole dataset in two corners of the plot. Is that even correct or did I code something wrong?

2. Is there another algorithm for clustering multidimensional data? I look at this but I can not find an approriate algorithm for clustering multidimensional data... How do I even implement e.g. Ward hierarchical clustering in python for my dataset?

3. Why should I use PCA for dimensionality reduction? Can I also use t SNE? Is it better?

1. the problem is that you fit your PCA on your dataframe, but the dataframe contains the cluster. Column 'cluster' will probably contain most of the variation in your dataset an therefore the information in the first PC will just coincide with data['cluster'] column. Try to fit your PCA only on the distance columns:

    data_reduced = PCA(n_componnts=2).fit_transform(data[['dist1', 'dist2',..., dist10']]
   

2. You can fit hierarchical clustering with sklearn by using:

    sklearn.cluster.AgglomerativeClustering()` 
   

   You can use different distance metrics and linkages like 'ward'

3. tSNE is used to visualize multivariate data and the goal of this technique is not clustering