How is Wikipedia's example of an unbalanced AVL tree really unbalanced?

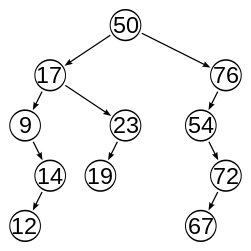
The image above is from "Wikipedia's entry on AVL trees" which Wikipedia indicates is unbalanced. How is this tree not balanced already? Here's a quote from the article:

The balance factor of a node is the height of its right subtree minus the height of its left subtree and a node with balance factor 1, 0, or -1 is considered balanced. A node with any other balance factor is considered unbalanced and requires rebalancing the tree. The balance factor is either stored directly at each node or computed from the heights of the subtrees.

Both the left and right subtrees have a height of 4. The right subtree of the left tree has a height of 3 which is still only 1 less than 4. Can someone explain what I'm missing?

To be balanced, every node in the tree must, either,

• have no children, (be a "leaf" node)
• Have two children.

• Or, if it has only one child, that child must be a leaf.

  In the chart you posted, 9, 54 & 76 violate the last rule.

Properly balanced, the tree would look like:

Root: 23
(23) -> 14 & 67
(14) -> 12 & 17
(12) -> 9
(17) -> 19
(67) -> 50 & 72
(50) -> 54
(72) -> 76

UPDATE: (after almost 9 years, I created a cool online chart for the graph at draw.io)